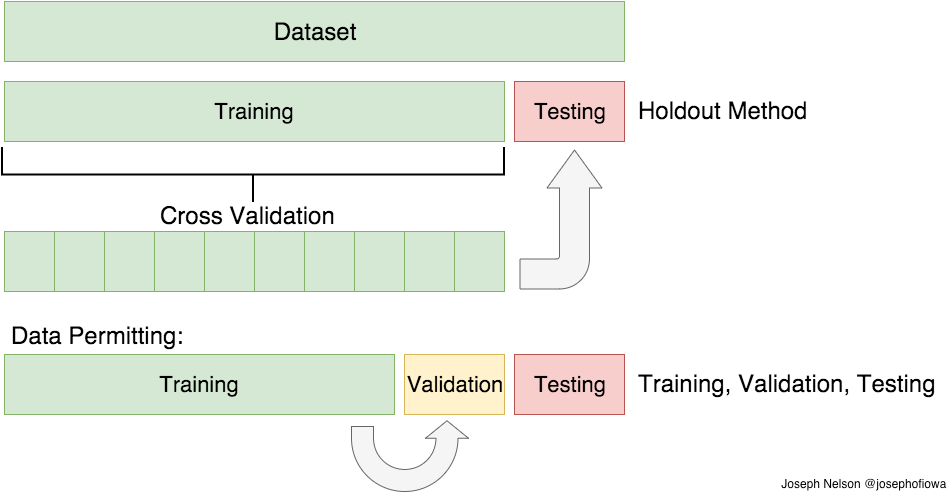
Chapter 5. Resampling Methods

5.1 Cross-Validation

5.1.1 The Validation Set Approach

• training set and validation set
• validation set error rate(typically MSE on quantitative)

drawback 1 : validation estimate of the test error rate can be highly variable

drawback 2 : In the validation approach, only a subset of the observations, so the validation set error rate may tend to overestimate the test error rate for the model fit on the entire data set

5.1.2 Leave-One-Out Cross-Validation

a single observation (x1, y1) is used for the validation set, and the remaining observations {(x2, y2), . . . , (xn, yn)} make up the training set. -> MSE1

MSE2 = (y2−ˆy2)2.

• the LOOCV estimate for the test MSE: the average of these n test error estimates

advantage1 : far less bias (not to overestimate)

advantage2: always yield the same results

if n is large : use the following formula(not always)

5.1.3 k-Fold Cross-Validation

• LOOCV is a special case of k-fold CV

• randomly dividing the set of observations into k groups, or folds, of approximately equal size. The first fold is treated as a validation set, and the mehtod is fit on the remaining k-1 folds

  

  

  • k = 5, k = 10 outputs would be similar to LOOCV
  • important to see the smallest test MSE than identify the correct level of flexibility

5.1.4 Bias-Variance Trade-Off for k-Fold Cross-Validation

• why k-fold CV » LOOCV?
  • computational advantage
  • bias-variance trade-off
    • bias : LOOCV « CV
    • variance : LOOCV(highly correlated) » CV

5.1.5 Cross-Validation on Classification Problems

• instead of MSE, number of misclassified observations

  

  where $E_{rri} = I(y_i \neq \hat{y_i})$

5.2 The Bootstrap

• to quantify the uncertainty associated with a given estimator or statistical learning method
• rather than repeatedly obtaining independent data sets from the population, instead obtain distinct data sets by repeatedly samply observations from the original data set.