CS231n 4강(혜주)

다음은 스탠포드 대학 강의 CS231n: Convolutional Neural Networks for Visual Recognition 을 요약한 것입니다.

4강의 내용을 도식화해서 정리하면 다음과 같습니다.

1. Back Propagation

3강에서 배웠던 optimization을 위해서는 gradient를 계산해야 합니다.그래서 이번 강의에서는 computational graph 에서 gradient를 계산하는 것을 배웁니다. input에 따른 W값,ouput 이 계산되면, 다시 앞으로 오면서 gradient를 계산합니다. 이 gradient를 참고해서 optimization이 이루어집니다.

###1) chain rule을 통한 gradient 계산

하단의 예제를 통해 이해해봅시다!

다음과 같은 식이 있다고 할 때, 하단의 gradient를 구하는 것은 chain rule을 사용하는 것입니다.

하단의 computer graph에서 output 쪽에 gradient는 1입니다.

f를 z로 미분하면 q이고 q = x+y이기 때문에 gradient는 3입니다.

f를 q로 미분하면 z이고 gradient는 -4입니다.

f를 y로 미분한 값은 chain rule을 통해 f의 q에 대한 미분과 q의 y에 대한 미분을 곱하면 얻을 수 있습니다. 즉 z*1 = -4입니다.

마찬가지로 f를 x로 미분한 값은 chain rule을 통해 f의 q에 대한 미분과 q의 x에 대한 미분을 곱하면 얻을 수 있습니다. 즉 z*1 = -4입니다.

이를 간단히 도식화하면

input을 통해 gradient를 얻게 되고, 연결된 바로 직전의 node에 gradient를 전달하게 됩니다. gradient는 local gradient와 upstream gradient를 구하여 이루어집니다.

더 복잡한 예제도 결국 chain rule을 통해서 구할 수 있습니다.(자세한 풀이는 생략)

• chain rule을 통한 gradient 계산의 장점

  어떠한 복잡한 node도 group화 시켜서 big node로 바꿀 수 있습니다. 예를 들어 sigmoid function의 경우, 미분하면 하단과 같은 형태로 나타나기 때문에 계산하면 0.2로 나타납니다. 즉 한번의 gradient 계산만 있으면 됩니다.

• vector로 확장

  

  ​

vector로 확장하면 jacobian matrix가 필요한데, 이것은 local gradient와 동일하다고 볼 수 있습니다.

그렇다면 input과 output이 4096 dimension인 경우 jacobian matrix는 어떠한 형태를 가질까요? 4096x4096 형태라고 볼 수 있습니다. 그러나 minibatch가 있는 경우 더 큰 크기의 행렬일 수 있습니다.

vector 형태로 gradient를 계산하는 것은 하단과 같은 결과를 보여줍니다. (과정은 복잡해서 생략..)

• forward/backward API

  

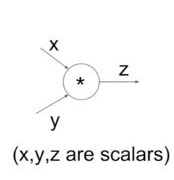
  상단과 같은 computational graph를 가진 경우 forward 와 backward를 계산하는 코드는 다음과 같습니다.

  class MultiplyGate(object):
    def forward(x,y):
      z= x*y
      self.x = x
      self.y = y
      return z
    def backward(dz):
      dx = self.y + dz #[dz/dx + dL/dz]
      dy = self.x + dz #[dz/dy + dL/dz]
      return [dx,dy]
  

  ​

  

  ​

2. Neural Networks 소개

그 전에는 linear한 score function하나만으로 계산했다면, Neural Networks는 W1,W2,W3..등 여러개의 layer를 가집니다. 그 사이에는 nonlinear한 function들로 연결됩니다. 그 예시들은 뒤의 강의에배우게 됩니다.

예를 들어 W1은 input과 직접적으로 관련된 템플릿이지만, W2는 score를 적절히 결합한 템플릿이라고 볼 수 있습니다.

• 2 layer의 Neural Network의 코드

  import numpy as np
  from numpy.random import randn
  
  N, D_in, H, D_out = 64, 1000, 100, 10
  x, y = randn(N, D_in), randn(N, D_out)
  w1, w2 = randn(D_in, N), randn(N, D_out)
  
  for t in range(2000):
    h = 1 / (1 + np.exp(-x.dot(w1)))
    y_pred = h.dot(w2)
    loss = np.square(y_pred - y).sum()
    print(t, loss)
      
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h.T.dot(grad_y_pred)
    grad_h = grad_y_pred.dot(w2.T)
    grad_w1 = x.T.dot(grad_h * h * (1 - h))
      
    w1 -= 1e-4 * grad_w1
    w2 -= 1e-4 * grad_w2
      
  

• ‘Neural Network’ 이름의 유래

  neuron의 자극 처리 메커니즘과 neural network의 메커니즘이 유사한 부분이 있기 때문입니다.

  input을 자극으로 생각하고 , 데이터를 처리하는 함수가 cell body로 볼 수 있습니다. activation function을 통해 결과값이 나오는 것도 유사하게 볼 수 있습니다. 하지만 정확히 뉴런의 메커니즘과 같지는 않으니 참고만 하면 됩니다.